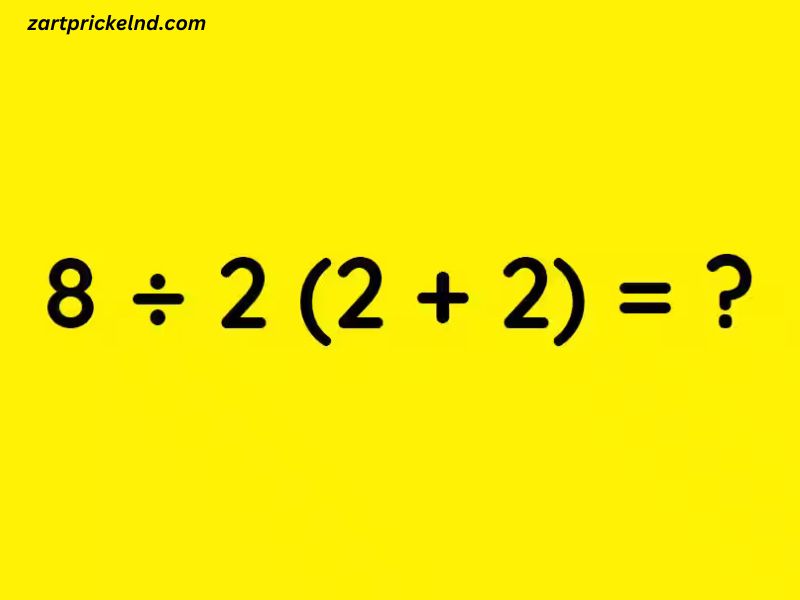Mathematics is a language that governs much of our understanding of the world, and its rules help ensure consistency and clarity in problem-solving. However, even the simplest mathematical expressions can sometimes provoke confusion. One such example is the expression 8/2(2+2), which has become notorious for the debates and confusion surrounding its interpretation. In this article, we will break down the steps, explain the rules, and explore the various ways in which this expression can be solved, while also addressing why different interpretations can lead to different answers.
Understanding the Expression: 8/2(2+2)
The expression in question is 8/2(2+2). Let’s look at each part to understand the fundamental operations:
- 8: This is a constant number.
- /2: This signifies division by 2.
- (2+2): This is a set of parentheses indicating that we need to first add 2 and 2 together.
At first glance, this seems straightforward, but the confusion arises from how to handle the order of operations, especially when it comes to interpreting the multiplication implied by the parentheses.
The Order of Operations: PEMDAS and BODMAS
To solve expressions like 8/2(2+2), we rely on established mathematical rules known as the order of operations. The two most common acronyms for these rules are PEMDAS and BODMAS, which stand for:
- PEMDAS: Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)
- BODMAS: Brackets, Orders (Exponents), Division and Multiplication (from left to right), Addition and Subtraction (from left to right)
The key takeaway from both of these acronyms is that multiplication and division, as well as addition and subtraction, should be handled from left to right. This is where the confusion often begins with expressions like 8/2(2+2), as the multiplication implied by the parentheses (after simplifying the terms inside) could be interpreted in two ways depending on how you read the expression.
Solving 8/2(2+2): Breaking It Down
To properly evaluate 8/2(2+2), let’s follow the order of operations step by step.
Step 1: Simplify the Parentheses
First, we simplify the expression inside the parentheses. In this case, 2+2 equals 4. The expression now looks like this:
8/2(4)
Step 2: Address Division and Multiplication
Now we need to apply division and multiplication. According to PEMDAS and BODMAS, multiplication and division are treated with equal precedence, meaning we should perform these operations from left to right. Therefore, we first divide 8 by 2, then multiply the result by 4.
- First, perform 8 ÷ 2, which equals 4.
- Now, multiply 4 by 4 (the result of 2+2).
This gives us:
4 * 4 = 16
So, the solution to the expression 8/2(2+2), using the correct order of operations, is 16.
Alternative Interpretation: A Look at Common Mistakes
Despite the clarity of the correct solution, many people are still prone to misinterpreting this expression. Some might argue that 2(2+2) should be treated as a single entity, and thus the expression should be read as:
8 / (2(2+2))
In this interpretation, you would first calculate the expression inside the parentheses (which we’ve already simplified as 4), then multiply it by 2, resulting in 8. This turns the expression into:
8 / 8 = 1
So, some might mistakenly conclude that the answer is 1, which is obviously incorrect according to the rules of order of operations.
Why This Happens: The Role of Ambiguity
The confusion surrounding the expression 8/2(2+2) highlights a deeper issue: the lack of parentheses to make the operation unambiguous. While the order of operations is clear, certain expressions can still be interpreted in multiple ways depending on how they are written or presented. When mathematical problems are written without proper notation, such as not clearly indicating multiplication or using ambiguous spacing, different interpretations can arise.
This particular expression is often cited as an example of how critical it is to write mathematical problems clearly and unambiguously. To avoid confusion, it’s always best to explicitly include parentheses to clarify the intended operations.
Why PEMDAS/BODMAS Isn’t Always Enough
Although PEMDAS and BODMAS are crucial guidelines for evaluating mathematical expressions, they are not always sufficient when it comes to parsing complex expressions that lack clarity. While these rules cover most cases, certain situations—like the 8/2(2+2) example—require further precision in how the expression is written to ensure a consistent interpretation.
In cases where division and multiplication appear together without clear parentheses, you should always rely on the convention of working from left to right. That said, it is essential to be mindful of how ambiguous expressions can be interpreted differently, especially when written informally or in a hurry.
Lessons from 8/2(2+2)
The famous 8/2(2+2) expression serves as a useful lesson in several important aspects of mathematical reasoning:
- Clarity in Notation: Always use parentheses to avoid confusion. Mathematicians and students alike should ensure that their expressions are written as clearly as possible to minimize misinterpretation.
- Order of Operations: Mastering PEMDAS/BODMAS is key to solving more complex expressions. Even when expressions are simple, it’s critical to follow the established rules and work through the operations step by step.
- Avoiding Assumptions: It’s easy to fall into the trap of assuming that multiplication or division should be performed in a certain way, but every step should be based on clear logical rules, not assumptions. Misreading the problem can lead to errors, as demonstrated by the alternative solution of 1.
- Communication in Math: In formal mathematics, clarity and precision are vital. In real-world scenarios, mathematical problems often need to be communicated to others—whether through textbooks, exams, or software—and clear notation can prevent unnecessary confusion.
Conclusion
In conclusion, the expression 8/2(2+2) has sparked much debate due to its potential for multiple interpretations. However, when following the correct order of operations—PEMDAS or BODMAS—the solution is clear: 16. This example highlights the importance of clarity in mathematical notation and how minor ambiguities can lead to different answers. By following the rules of operation carefully, practicing clear expression, and avoiding assumptions, one can solve mathematical problems more efficiently and accurately.
While this expression may seem simple, it offers an excellent reminder that even the most basic of equations can be subject to interpretation, and clear communication in mathematics is as important as the math itself.